


MÓDULO DE MATEMÁTICAS
Tomado de http://akifrases.com/frase/189364
Direccionamiento a páginas con material importante. Respeto por los derechos de autor.
Un espacio para las Matemáticas
Teorema de Apolonio (teorema de la mediana)
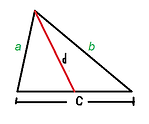
El Teorema de o teorema de la mediana, relaciona la longitud de la mediana de un triángulo con las longitudes de sus lados.
Para todo triángulo la suma de los cuadrados de dos lados cualesquiera, es igual a la mitad del cuadrado del tercer lado más el doble del cuadrado de su mediana correspondiente.
El Teorema de Stewart se puede aplicar para hallar la longitud de una mediana de un triángulo en función de los lados del triangulo.


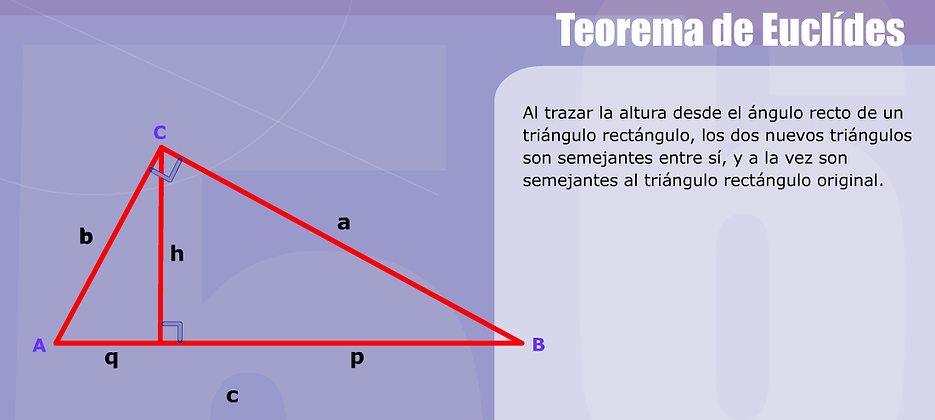
Teorema de Euclides
Presentación Educar Chile:
El teorema de señala que en todo triángulo rectángulo se cumple que:
-
el cuadrado de la altura sobre la hipotenusa es igual al producto de las proyecciones de los catetos sobre la hipotenusa (teorema de la altura).
-
el cuadrado de un cateto es igual al producto de la hipotenusa por la proyección del cateto sobre la hipotenusa (teorema del cateto).

Teorema de Pitágoras
El teorema de establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos.
Dado un triángulo rectángulo ABC, con lados a y b, los catetos correspondientes y c, su hipotenusa, tenemos:

EL TEOREMA DE PITÁGORAS EN UNA SUPERFICIE ESFÉRICA


TEOREMA DE HERON
Físico y matemático griego que vivió en Alejandría en una época no exactamente determinada de los siglos I y II d. de C. Son conocidas varias obras suyas, entre muchas se le recuerda por una fórmula para hallar el área de cualquier triangulo, conocidos sus lados. Si llamamos A el área del triángulo, p al semiperímetro y a, b, c a los tres lados:


POTENCIA DE PUNTO
La potencia de un punto hace referencia a las longitudes de segmentos de rectas que pasan por dicho punto y cortan a una circunferencia.
Punto interior a la circunferencia:
Dados los segmentos AB, CD, FE, que se cortan en el punto p, al interior de una circunferencia se cumple que:
PA.PB=PC.PD=PE.PF
Euclides en los Elementos, señaló: “Si en una circunferencia se cortan dos rectas entre sí, el rectángulo comprendido por los segmentos de una es igual al rectángulo comprendido por los segmentos de la otra”.
Dadas las rectas secantes AB Y CD que se intersecan en un punto P exterior a la circunferencia, entonces:
PA.PB=PC.PD
Punto a una secante y una tangente
Dada una recta secante a una circunferencia, con corte en los puntos A y B; y una recta con punto de tangencia en T, se tiene:
PA.PB=PT²



TEOREMA DE LA BISECTRIZ EXTERIOR
TEOREMA DE LA BISECTRIZ EXTERIOR
La bisectriz de un ángulo exterior, divide a la prolongación del lado opuesto en dos segmentos EB y EC directamente proporcionales a los lados AB Y AC que forman dicho ángulo.
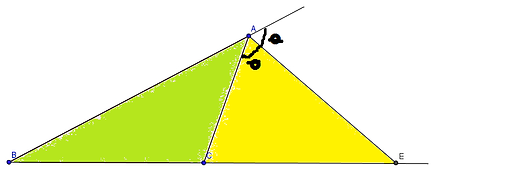
En el triángulo ABC, se ha trazado la bisectriz exterior en la prolongación del lado AB, hasta la prolongación del lado AC.

El trazo de la bisectriz exterior siempre va ser único y siempre relativo al menor lado, es decir se prolonga al mayor lado para el trazo de la bisectriz, para establecer la relación entre el mayor y el menor lado del triángulo.
TEOREMA DE LA BISECTRIZ INTERIOR
La bisectríz de un ángulo de un triángulo divide al lado opuesto en dos segmentos proporcionales a los lados que forman este ángulo.
